4.1.7 单层卷积网络（one layer of convolutional network）

单层神经网络的原理

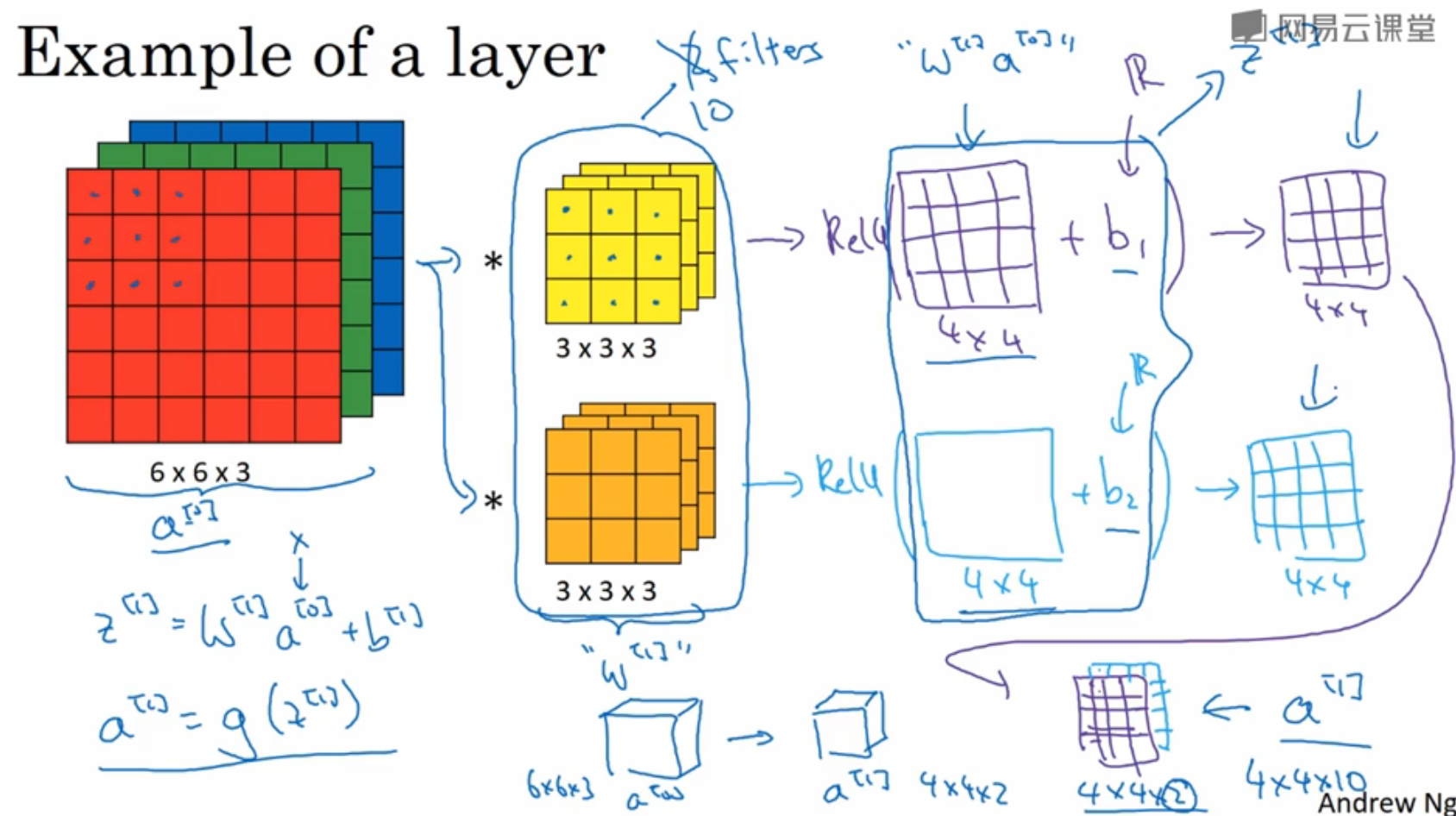
首先看到一个$$663$$的RGB图像（矩阵A），有两个过滤器，分别对应提取图像不同的特征。 两个过滤器会带来两个不同的的输出，根据输出矩阵的阶数关系，$$663$$与$$333$$的矩阵进行卷积操作之后，会得到$$441$$的矩阵（矩阵E）。 之后我们为$$E_1$$与$$E_2$$分别加上偏差$$b_1$$、$$b_2$$，然后在应用非线性函数$$E_1=k_e(E_1+b_1)$$,得到最终输出的新矩阵$$E_1$$与$$E_2$$，再将$$E_1$$与$$E_2$$合并为一个$$442$$的矩阵即为最终输出。 同样的，若上述卷积过程使用了10个过滤器，则会输出一个$$4410$$的矩阵。

避免过拟合（overfitting）

//todo 还不太懂这个地方

卷积神经网络常用的记号

若这是一层卷积层

• $$f^{[l]}$$：过滤器的大小（filter size），$$l$$表示这是第几层。
• $$p^{[l]}$$：padding，$$l$$表示这是第几层。
• $$s^{[l]}$$：步长（stride），$$l$$表示这是第几层。
• $$n^{[l]}$$: 过滤器的数量2

输入与输出的]关系

若输入是一个$$n{h}^{l-i}*n{w}^{l-i}*n_{h}^{l-i}$$的矩阵，则对应的输出为$$n^{[l]}=\frac{n^{[l]}-f^{[l]}+2p^{[l]}}{s^{[l]}}+1$$，输出矩阵的高（h）,宽（w）以及通道数（c）都可以用上述公式算出来

每一层的过滤器的阶数

输入矩阵的通道数要与过滤器的通道数相同，数学表示为过滤器的阶数为$$n{h}^{l}*n{w}^{l}*n_{h}^{l-i}$$

偏差（bias）

偏差是一个实数为了方便，经常使用一个$$111*n_{c}^{l}$$的向量表示偏差